La teoría de la relatividad
La teoría de la relatividad irá siempre ligada al nombre de Albert Einstein, así que en primer lugar presentaremos brevemente a este científico tan excepcional.
Einstein fue un alemán de origen judío, y aunque forma parte de la historia de la ciencia, siempre ha habido rumores de que fue un mal estudiante. Estos son, sin embargo, totalmente infundados.
Es cierto que centró todo su interés en las ciencias, lo que le hizo obtener algunos malos resultados en otras asignaturas, pero aun así se diplomó como profesor de ciencias físicas y matemáticas y realizó un doctorado en física.
Las circunstancias de la vida le llevaron a trabajar en una oficina de patentes, y fue en esa época, mientras pasaba las horas en el despacho, en la que escribió la famosa teoría de la relatividad.
La desarrolló en dos etapas; la teoría de la relatividad especial, en 1905, y la teoría de la relatividad general entre 1915 y 1916.
La diferencia entre ambas es, a grandes rasgos, que en la primera versión no se aplica el efecto de la gravedad, y en la versión general sí que incluye este factor.
- Teoría de la relatividad especial:
Empezaremos explicando de manera sencilla lo que la propia palabra describe, la relatividad.
Para nuestra lógica, el tiempo, la energía y el espacio son absolutos; un metro siempre mide un metro, un segundo siempre dura un segundo, etc. Pero esto solamente es cierto siempre que todos los actores estén en un mismo sistema de referencia.
Esto nos lleva al primer postulado de Einstein en que nos expone precisamente esto.
Todas las leyes fundamentales de la física se cumplen siempre y cuando todos los observadores se encuentren en un mismo sistema de referencia. Y este sistema de referencia debe estar en reposo o moverse a una velocidad constante.
Pongamos algunos ejemplos.
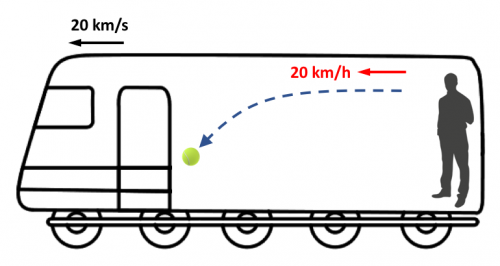
Nos encontramos dentro de un vagón en un tren en movimiento uniforme a una velocidad de 20 km/h.
Si tiramos una pelota hacia delante a 20 km/h, la pelota irá a esa misma velocidad para cualquiera observador que se encuentre dentro del vagón.
Si en vez de lanzar la pelota la dejamos caer en vertical hacia el suelo del tren, también caerá en vertical para todos los que se encuentren dentro.
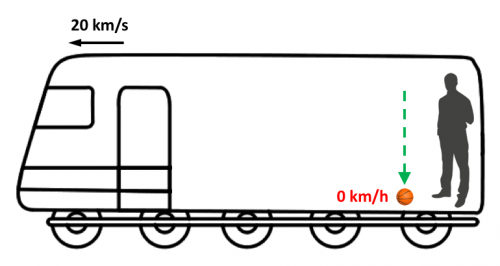
En este caso, nuestro sistema de referencia es el vagón y todo lo que contiene, y como vemos, las leyes de la física se cumplen perfectamente y por igual para todo el que está en su interior.
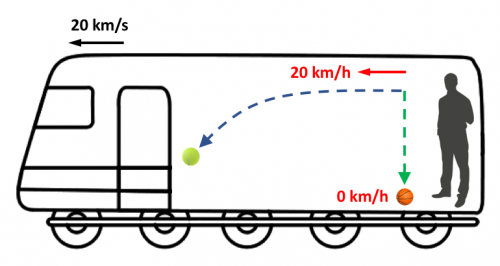
Cambiemos ahora algunos parámetros.
Supongamos que el vagón es transparente y que desde fuera solo se ve el movimiento de las pelotas.
También cambiaremos de sistema de referencia, y en este caso los observadores se encuentran fuera del vagón, por ejemplo, en la estación de trenes.
Nosotros seguimos dentro del vagón en movimiento, y volvemos a repetir los dos lanzamientos de las pelotas.
Primero lanzamos la pelota hacia delante a 20 km/h.
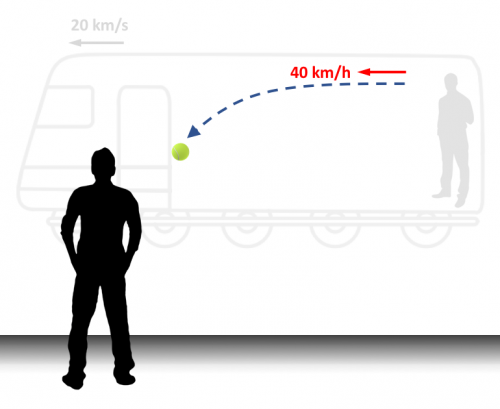
Para nosotros nada cambia, pero para el observador de la estación la pelota se mueve hacia delante a 40 km/h.
Su sistema de referencia es la estación, por lo que la pelota se mueve a 20 km/h del movimiento del tren más los 20 km/h del lanzamiento.
Seguidamente dejaremos caer en vertical la segunda pelota, también igual que en el primer ejemplo.
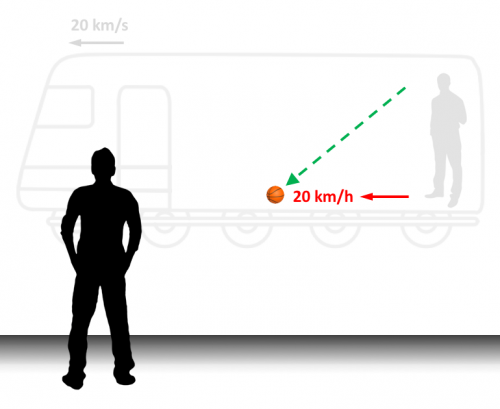
Ahora el observador externo verá moverse la pelota a 20 km/h hacia delante.
Y estos serían, por lo tanto, los dos movimientos que describiría el observador de la estación.

Como podemos comprobar, si nosotros y el observador de la estación describiéramos lo que hemos visto, ambos explicaríamos dos cosas totalmente distintas, aunque se trate de los mismos sucesos.
Sin embargo los dos tendríamos razón.
Veamos otro ejemplo.
En este caso, desde dentro del vagón, volveremos a lanzar la primera pelota a 20 km/h pero esta vez en dirección contraria al movimiento del tren.
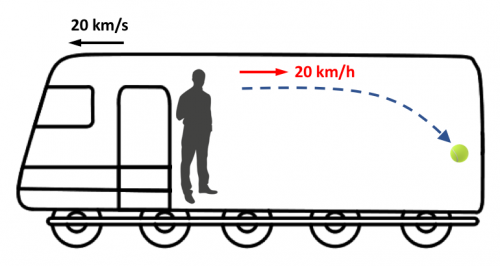
Y de nuevo dejaremos caer la otra pelota en vertical hacia el suelo.
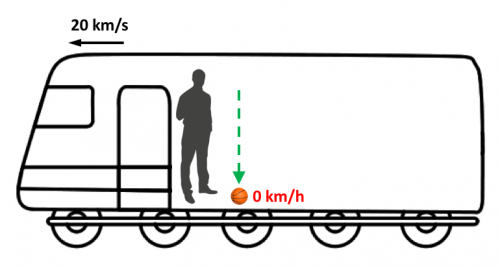
Para nosotros, que estamos dentro del tren, todo es exactamente igual que en el primer ejemplo, y seguimos viendo como las pelotas se mueven exactamente como las hemos tirado.
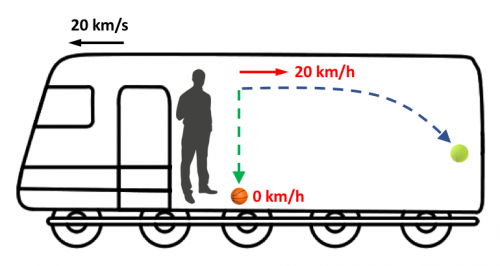
Veremos una pelota que se aleja a 20 km/h, esta vez hacia la parte trasera del vagón, y otra que cae en vertical hacia el suelo.
Volvamos entonces a nuestro observador externo.
Si analizamos lo que ve desde el exterior, con la estación como sistema de referencia, vemos que de nuevo tenemos un resultado totalmente distinto, incluso sorprendente.
Para el observador de la estación, la pelota que hemos lanzado a 20 km/h en dirección contraria al movimiento del tren, cae verticalmente hacia el suelo.

Y la pelota que hemos dejado caer hacia el suelo, igual que en el primer ejemplo anterior, se mueve a 20 km/h en la dirección del movimiento del tren.
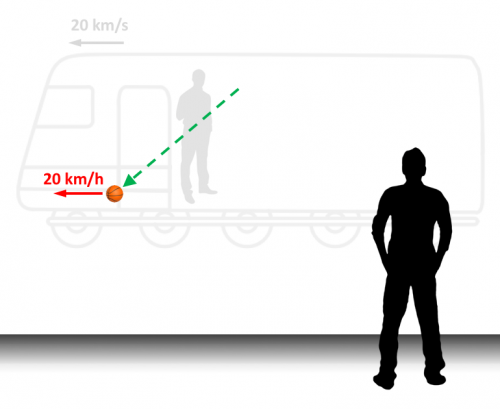
De nuevo, el escenario de ambas pelotas es totalmente diferente para el espectador de la estación que para nosotros.
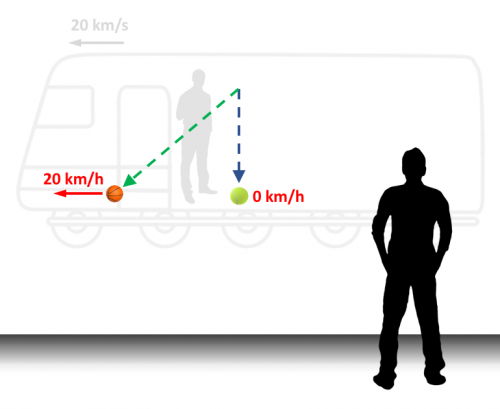
Estos ejemplos describen perfectamente la relatividad entre ambos escenarios, y que, como describió Einstein, las leyes físicas solo son absolutas dentro de un sistema de referencia.
Esto llevó a Albert Einstein a intentar extrapolar la situación, pero en vez lanzar una pelota, lanzando un rayo de luz.
Volviendo a la situación en que estamos en el interior del vagón, lanzaremos un rayo de luz en la dirección del movimiento del tren. Para nosotros, el rayo de luz se desplazará a la velocidad de la luz, es decir, a 299.792 km/s en la dirección del movimiento del tren. Y si lanzamos el rayo de luz en dirección contraria al movimiento también se desplazará a la misma velocidad.
Hasta aquí todo sucede como esperado.
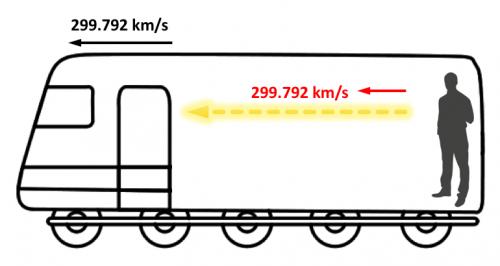
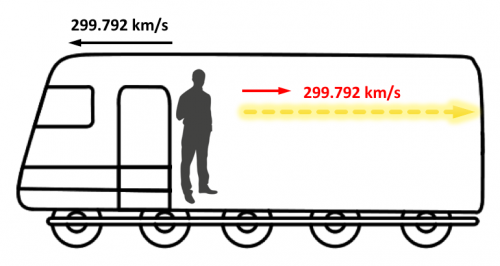
Pasemos ahora al caso del observador exterior, y para que el experimento sea parecido al anterior y los resultados sean muy evidentes, supondremos que el tren se desplaza también a la velocidad de la luz.
En el primer caso, con la luz moviéndose en la dirección del tren, el rayo de luz debería viajar a casi 600.000 km/s respecto al observador exterior, ya que se sumaría la velocidad propia del rayo de luz y la velocidad a la que viaja el tren.
Y el rayo enviado en dirección contraria al movimiento del tren, puesto que las dos velocidades se compensan, debería verse… ¿inmóvil?.
Evidentemente, estas condiciones no son reproducibles para comprobarlo empíricamente, sin embargo, al plantearse la situación, Einstein supo que esto violaría las ecuaciones de Maxwell. Estas indican que cualquier radiación electromagnética se mueve siempre a la velocidad de la luz, independientemente del sistema de referencia, y la luz se trata de una radiación electromagnética.*
*Las radiaciones electromagnéticas se mueven a la velocidad de la luz en el vacío, por lo que en nuestros ejemplos las velocidades deberían ser un poco más bajas, pero los escenarios son perfectamente representativos.
Esto llevó a Einstein a proponer que la velocidad de la luz sí que se trataba de un valor de medida absoluto.
Es decir, que fuera cual fuera el sistema de referencia en que la midiéramos, siempre tendría el mismo valor.
Por tanto, en los dos casos anteriores, para el observador de la estación, la luz seguiría moviéndose a 299.792 km/s, exactamente igual que para nosotros que nos encontramos en el interior del vagón.
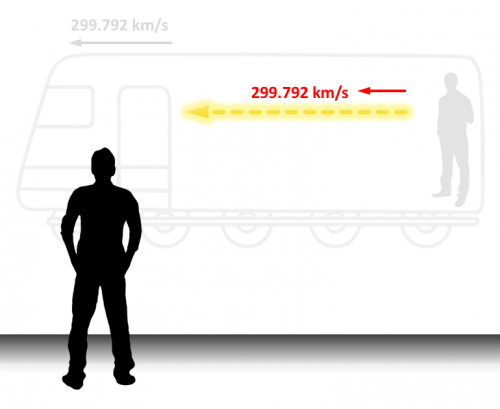
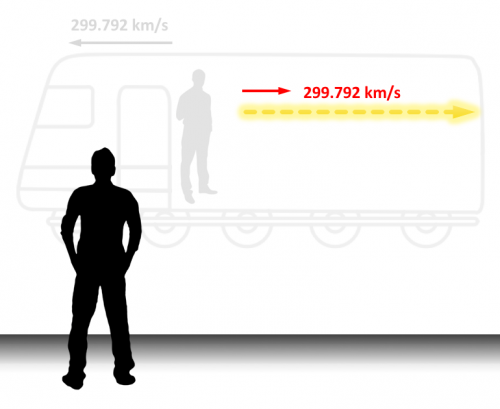
Parece que esto se contradiga con los primeros casos, ya que si partimos del ejemplo de las pelotas y vamos aumentando la velocidad con que las lanzamos, seguiríamos teniendo diferencias entre el observamos del vagón y el de la estación.
¿Como es posible, entonces, que esto deje de cumplirse cuando nos acercamos a la velocidad de la luz?
Precisamente esto fue lo que llevo a Einstein a desarrollar su teoría.
En ella describió que para que la velocidad de la luz tenga un valor absoluto, a medida que tratamos con velocidades cada vez más altas, lo que debe variar son el tiempo y el espacio.
Más concretamente, el tiempo se dilata y el espacio se contrae, lo que nos explica el porqué de la famosa expresión “el espacio-tiempo”.
Este fue su segundo postulado para la relatividad especial; la velocidad de la luz es una constante universal.
Esta teoría sobre la relatividad del espacio y del tiempo está sobradamente demostrada en la actualidad, y aunque en nuestra vida cotidiana no podemos apreciarlo, es imprescindible, por ejemplo, para asegurar el correcto funcionamiento de los satélites responsables del GPS.
A partir de la hipótesis de la velocidad de la luz como una constante, Einstein postuló también la equivalencia entre masa y energía. La masa se puede transformar en energía y viceversa, y lo hacen siguiendo la que es, seguramente, la fórmula más famosa de la historia de la ciencia:
E = mc²
- Teoría de la relatividad general:
Como hemos comentado anteriormente, 10 años después de la relatividad especial, Einstein publicó la Teoría de la relatividad general.
En este caso es mucho más complicado poner ejemplos prácticos para describirla, pero vamos a explicar que factores nuevos intervienen para intentar entender lo que aporta esta nueva versión de la relatividad.
En primer lugar debemos recordar que la relatividad especial no es aplicable a sistemas donde el campo gravitatorio desempeña un papel importante, y es, por tanto, incompatible con la teoría de la gravitación universal de Isaac Newton, que explicaba el funcionamiento de las grandes masas del universo.
Como hemos visto, en situaciones ocurridas sobre la Tierra sí podemos aplicar la relatividad especial ya que, aunque pueda parecer que la tierra tiene un campo gravitatorio importante, a niveles cosmológicos es prácticamente despreciable.
Cuando hablamos de campos gravitatorios importantes nos referimos a los generados por grandes cuerpos celestes, como las estrellas, las galaxias o los agujeros negros.
Y aquí tenemos otra de las grandes aportaciones de Einstein. Propuso que la gravedad no se trataba realmente de una fuerza, sino de una curvatura del espacio-tiempo generada por la presencia de una masa.
Por esta razón ya no se habla de la fuerza de la gravedad, sino de campos gravitatorios.
¿Y qué quiso decir Einstein con esto?
Einstein explicó que la presencia de una masa muy grande produce una deformación del espacio, curvándolo.
Aquí, lo más importante es comprender que si es el espacio lo que se curva, una línea recta que pase por dicho espacio se convertirá también en una línea curva, pero sin embargo, seguirá siendo el camino más corto entre dos puntos.
¿Y cómo se puede representar con un ejemplo sencillo la acción de la gravedad curvando el espacio?
Seguramente con una imagen que habéis visto muchas veces.
Supongamos el espacio como una superficie plana.

Si lanzamos un rayo de luz se moverá en línea recta a través del espacio.

Si en este espacio encontramos un cuerpo con una masa suficientemente grande, éste se deformará curvándose hacia la propia masa.

Si en presencia de este cuerpo masivo lanzamos de nuevo el rayo de luz, éste solo puede viajar por el espacio, por lo que también se vería afectado por esta deformación.

Cuanto mayor sea la masa del cuerpo, mayor será la curvatura que se producirá en el espacio que le rodea.
Podemos verlo en la siguiente imagen.

Por esta razón, la deformación que produce el Sol en el espacio es mayor que la de la Tierra, y la de la Tierra mayor que la de la Luna.
Si volvemos al ejemplo del rayo de luz que viaja a través del espacio, puesto que lo hace a muchísima velocidad, cuando se encuentra una deformación producida por la gravedad, deformará su trayectoria, pero seguirá su camino.
Es lo mismo que sucedería si lanzamos una bola rodando por el suelo y se encuentra un agujero en el suelo. Si su velocidad es suficientemente alta curvará su trayectoria, pero continuará su recorrido.

Si embargo, si la velocidad de la bola no es suficiente, acabará cayendo hacia la deformación del espacio.

Siguiendo con este ejemplo podemos explicar el movimiento de la tierra alrededor del Sol.
Si la pelota lleva una velocidad que no le permite escapar de la curvatura, pero lo suficientemente alta como para no caer hacia ella gracias a la fuerza centrífuga, podría quedarse girando alrededor de la deformación.

Si en este caso no hubiera rozamiento, la bola se quedaría dando vueltas alrededor de la deformación, que es exactamente lo que pasa con la Tierra alrededor del Sol.
Cuando decimos que la Tierra está atrapada por el campo gravitatorio de Sol, en realidad está atrapada en la curvatura del espacio que este crea a su alrededor.
Este fenómeno es el mismo que permite a la luna o a los satélites artificiales orbitar alrededor de la Tierra.
La velocidad debe llevar un cuerpo y que permite este equilibrio entre la fuerza centrifuga y la atracción de la gravedad es lo que conocemos como velocidad orbital.

Si el Sol, que es una estrella mediana, consigue curvar el espacio lo suficiente como para mantener a la Tierra orbitando a su alrededor, imaginemos la curvatura que pueden generar cuerpos que son millones de veces más masivos.
Aquí vemos un ejemplo comparativo entre la curvatura que generaría una estrella como el Sol, una enana blanca y un agujero negro.
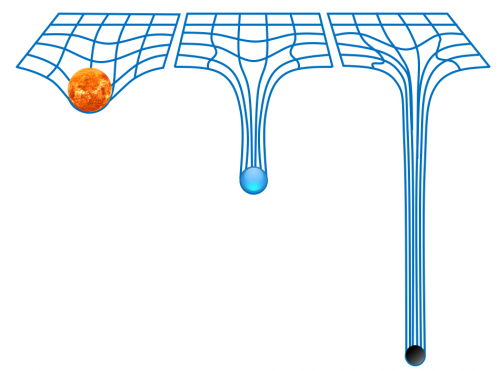
De hecho, los objetos más masivos que se conocen son los agujeros negros, y producen una deformación tan pronunciada del espacio que, incluso la luz cae hacia su interior si pasa lo suficientemente cerca.
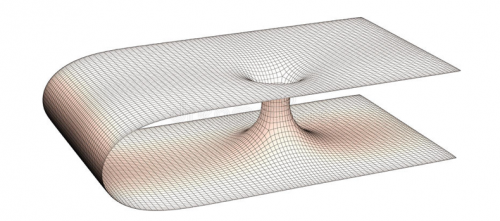
Hay hipótesis matemáticas que sostienen que un agujero negro con a la suficiente masa, podría curvar tanto el espacio que este llegaría a doblarse sobre sí mismo, uniendo lugares muy distantes en el universo creando lo que conocemos como agujeros de gusano.
Estas teorías, sin embargo, no están demostradas, y no se sabe prácticamente nada sobre lo que sucede en el fondo de un agujero negro.
- El eclipse de 1919:
Einstein fue un científico avanzado a su tiempo y su teoría de la relatividad era totalmente revolucionaria y muy difícil de demostrar. Sin embargo, todos los experimentos que se han realizado posteriormente han confirmado sus hipótesis.
Uno de los primeros fue realizado por un equipo inglés en 1919. El ensayo pretendía demostrar la curvatura del espacio predicha por Einstein. Si la teoría era correcta, la masa del Sol del debería curvar la luz de las estrellas que pasa cerca de él.

Para ello, debían estudiar estrellas que estuvieran detrás del Sol de manera que la luz llegara a la Tierra tras curvarse al verse afectada por la masa solar.

Esto, sin embargo, era muy complicado, ya que era imposible distinguir la luz de la estrella justo alrededor del Sol debiendo realizar el experimento a plena luz del día.
La solución fue realizar la observación durante un eclipse solar, momento en que el cielo está oscuro y se puede ver perfectamente el espacio que rodea al Sol.

Se programó realizar el experimento durante el eclipse previsto para el 29 de mayo de 1919, y decidieron estudiar la luz de un cúmulo de estrellas llamado Híades que en ese momento se encontraría oculto detrás del Sol…

…y que, por tanto, durante el eclipse no “debería” poder observarse desde la Tierra durante el eclipse.

Cuando llegó el día del eclipse y realizaron la observación, la luz de las Híades apareció exactamente donde estaba previsto según la curvatura del espacio de la ley la relatividad.

Las Híades aparecían en una localización aparente, ya que en ese momento se encontraban ocultas detrás del Sol. Cuando hablamos de localización aparente es porque en realidad vemos la estrella en una situación que no es real, ya que nuestra lógica nos indica que la luz viaja en línea recta.
Podemos verlo claramente en el esquema:

Respecto a los observadores la posición real de las Híades era en esta posición, justo detrás del Sol.

Este experimento ha sido repetido posteriormente en múltiples ocasiones, ya con métodos mucho más modernos y más precisos, confirmando siempre que la teoría de la relatividad es correcta.