El efecto Doppler
Quizás el título no os suene, pero seguro que algunos ejemplos que utilizaremos para explicarlo sí que os son más familiares.
El efecto Doppler es el responsable de como cambia el sonido de una ambulancia cuando se acerca o se aleja de nosotros y también está relacionado con el efecto de los aviones cuando rompen la barrera de sonido.
Aquí describiremos ambos casos, pero para entenderlos bien empezaremos aclarando algunos conceptos esenciales sobre este fenómeno.
Como la mayoría de los descubrimientos de la ciencia, el efecto Doopler debe su nombre al físico que lo describió por primera vez en 1842, Christian Andreas Doppler.
Afecta a todo tipo de ondas, pero con los casos de la ambulancia y del avión nos centraremos en las ondas sonoras.
Pero, ¿Qué es y cómo funciona una onda?
Lo primero que debemos tener muy claro es que una onda es un fenómeno que únicamente desplaza energía, y nunca materia.
Esto se ve claramente utilizando una cuerda. Si la hacemos ondular cogiéndola desde un extremo, vemos que esta se mueve de arriba abajo y la energía que le damos con la mano se traslada hasta el final de la cuerda, pero la cuerda está siempre en el mismo sitio.

Otro ejemplo interesante son las ondas que se producen en el agua cuando tiramos una piedra.
Este caso es un poco más confuso. A primera vista da la impresión de que el agua se desplaza desde el lugar de impacto de la piedra hacia el exterior, sin embargo, no lo hace.
El agua solo sube y baja, igual que la cuerda en el ejemplo anterior, y las ondas se propagan trasladando solo energía.

De hecho, si cortáramos una sección de la foto anterior, veríamos que el efecto es exactamente el mismo que al ondular la cuerda.

Y finalmente llegamos a las ondas sonoras, que son las que veremos aquí, y que funcionan de la misma manera.
En el primer ejemplo las ondas se movían a través de la cuerda sin moverla, en el segundo las ondas se propagaban a través del agua también sin desplazarla y en el caso de las ondas del sonido, estas se propagan a través del aire haciéndolo vibrar, pero también sin desplazarlo.
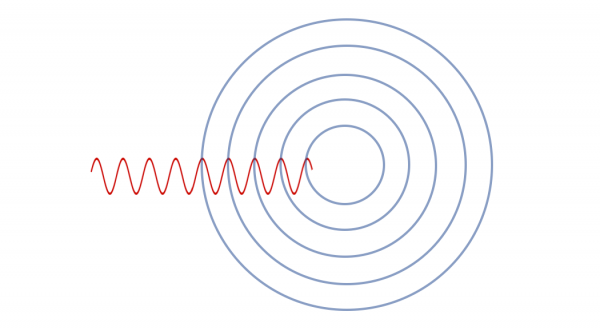
Las ondas sonoras siempre provienen de un foco de emisión y se propagan en todas las direcciones. Se verán, por tanto, como esferas concéntricas que van desplazándose hacia el exterior del foco.

Sin embargo, para simplificarlo se suele representar con círculos concéntricos alrededor del origen.

Todas las ondas se pueden representar con una función sinusoidal (como el movimiento de la cuerda) y las ondas sonoras no son una excepción. De hecho, es exactamente lo que hacen los ecualizadores de sonido que estamos acostumbrados a ver en nuestros equipos de música.

Aquí vemos como se relacionaría la función sinusoidal con la representación de los círculos concéntricos que vimos anteriormente.
En el gráfico del ecualizador vemos que la forma de las ondas puede variar mucho, y esto se debe a que los sonidos pueden tener mayor o menor volumen y pueden tener tonos más altos o más bajos.
Estas variaciones en el sonido vienen definidas por ciertas características de las ondas sonoras:
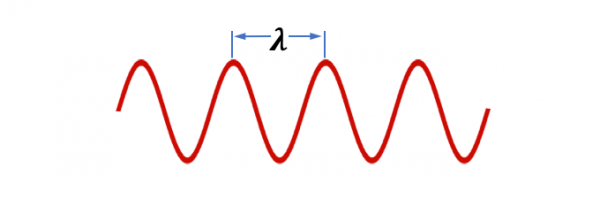
La longitud de onda (λ), es la distancia entre las cumbres de las ondas.
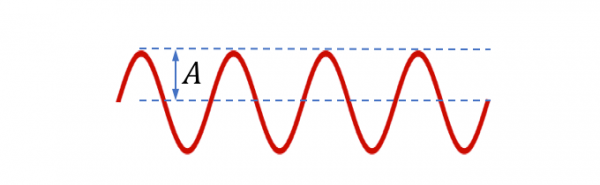
Cuanto mayor es la amplitud de la onda, mayor es el volumen del sonido.
- Sonido más débil:

- Sonido más fuerte:
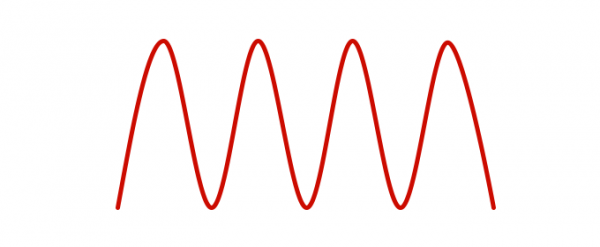
El período (T), es el tiempo que tarda cada uno de los puntos en recorrer una longitud de onda o, dicho de otra manera, lo que tarda cada punto de la onda en volver al mismo estado.
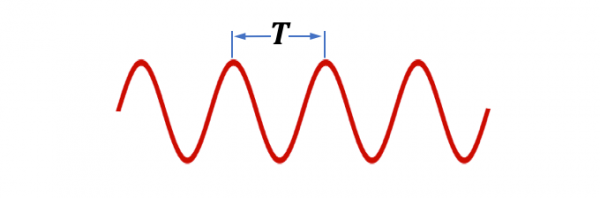
Que para las ondas del sonido también podría representarse así:

La inversa del período es lo que llamamos frecuencia, que es la cantidad de frentes de onda por segundo. Corresponde al tono del sonido.
Por ejemplo, las notas musicales tendrán una frecuencia diferente cada una.
f=1/T
Cuanto más alta es la frecuencia más aguda es el sonido y viceversa.
- Sonido más agudo:
- Sonido más grave:

Por último, tenemos la velocidad de propagación (v), que es la velocidad a la que se traslada la energía y se obtiene se multiplicar la longitud de onda por la frecuencia
La velocidad de un tipo de onda es constante a no ser que cambiemos el medio en que se propaga
v=λx f
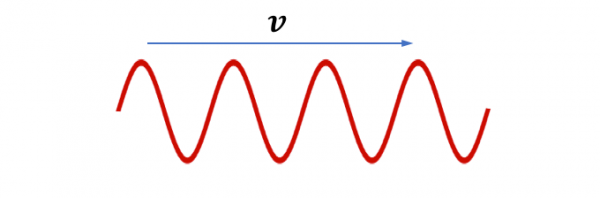
Por ejemplo, las ondas del sonido se propagan a 343,2 m/s (1.235 km/h) en el aire, bajo el agua es de 1.540 m/s (5.734 km/h) y en el acero es de 6.100 m/s (82.960 km/h).
La velocidad del sonido en el aire es, por lo tanto, constante, y también se llama Mach 1. Esta nomenclatura se utiliza mucho en aviación, por lo que un avión que puede volar al doble de la velocidad del sonido se dice que alcanza Mach 2.
Las características que hemos visto describen como son las ondas, y centrándonos en las ondas sonoras, la frecuencia es el factor clave para entender el efecto Doppler.
De hecho, el efecto Doppler se define como el cambio de frecuencia aparente de un sonido en movimiento para un observador. O lo que es lo mismo, el cambio de tono que notamos en un sonido cuando el emisor del sonido se acerca o se aleja.
Veamos ahora en detalle los ejemplos que pusimos al principio.
El caso más cotidiano es cuando vemos pasar una ambulancia por delante de nosotros.
- Si la ambulancia estuviera parada oiríamos el sonido de la sirena con su tono original.
- Cuando la ambulancia se mueve hacia nosotros oímos un sonido mucho más agudo.
- Cuando la ambulancia se aleja de nosotros oímos un sonido mucho más grave.
Estas diferencias se deben precisamente al efecto Doppler.
Empecemos por el caso de la ambulancia parada respecto a nosotros.
En este caso, el sonido nos llega con la frecuencia original de la sirena y supondremos que son 800 Hz (hercios).
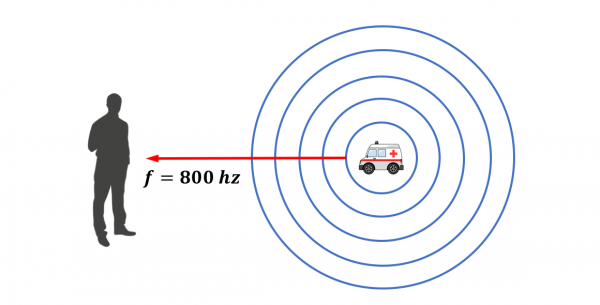
Como vemos en el gráfico, la frecuencia de la onda que sale de la ambulancia cuando está parada es igual hacia todos los lados y será la que recibiremos, independientemente de donde nos situemos respecto a la ambulancia.
Oiremos, entonces, un sonido con un tono de 800 Hz.
Veamos ahora el mismo caso con la ambulancia moviéndose hacia nosotros a 54 km/h.
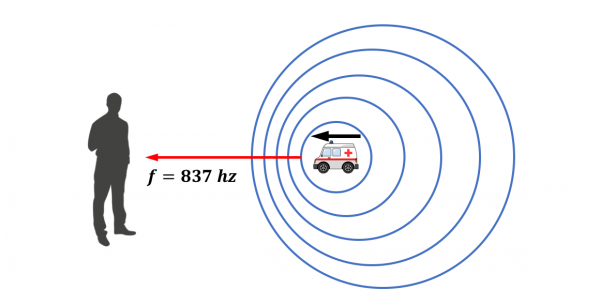
En este caso vemos que las ondas que emite se van apelotonando en su parte delantera, con lo que el sonido que nos llegará a nosotros tendrá una longitud de onda más pequeña que lo original y por tanto, mayor frecuencia.
Recordad que hemos comentado que la velocidad de una onda es constante, si disminuye la longitud de onda tiene que aumentar la frecuencia.
v=λ↓x f↑
Haciendo los cálculos vemos que el sonido que recibiremos tiene una frecuencia de unos 837 Hz, lo que significa que nos llegará un sonido más agudo que cuando la ambulancia estaba parada.
Y finalmente miremos lo que sucede si la ambulancia se aleja de nosotros:
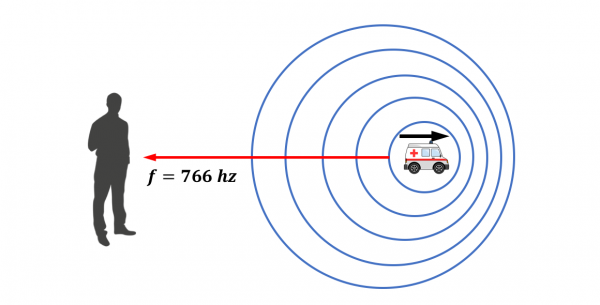
Como vemos aquí, el efecto es el contrario al anterior, el sonido que recibimos tiene una longitud de onda mayor que el original.
En este caso, entonces, el sonido nos llega con una frecuencia más baja (766 Hz), por lo que oiremos la sirena con un tono más grave.
v=λ↑x f↓
Estas tres circunstancias explican perfectamente el efecto Doppler, y el caso de la ambulancia lo experimentamos a menudo en nuestra vida diaria.
Cuando la vemos venir hacia nosotros oímos la sirena muy aguda, y cuando se aleja, después de pasar, vemos que el sonido se convierte en mucho más grave.
Si combinamos los esquemas anteriores podemos ver representada la diferencia de sonido que percibimos entre ambas situaciones.

Una vez visto esto entenderemos muy bien el segundo ejemplo que habíamos puesto.
¿Qué significa romper la barrera del sonido?
Cambiemos la ambulancia por un avión, y supongamos que este avión se mueve exactamente a la velocidad del sonido, es decir a Mach 1.
En este caso el avión iría a la misma velocidad que los frentes de onda que emite, y lo podríamos representar de la siguiente manera:
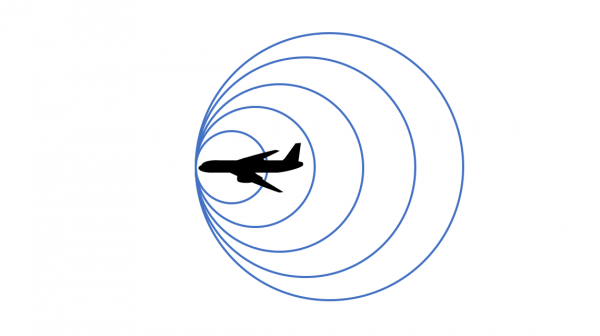
Esta circunstancia hace que los frentes de onda se vayan solapando unos con otros.
Si el avión continúa acelerando y supera la velocidad del sonido adelantará a las ondas que el mismo emite. Es entonces cuando el avión rompe la barrera del sonido.
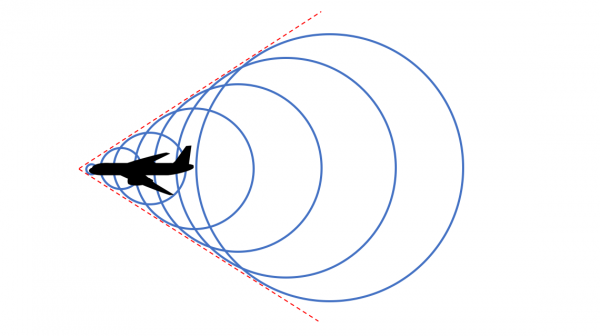
En el momento en que se rompe la barrera del sonido y el avión atraviesa el frente de ondas se produce un fuerte estallido que se denomina explosión sónica, y tras ella el avión va dejando atrás las ondas que genera. Esto, como vemos en el dibujo, produce un efecto que se llama conificación.
El piloto, al ir más rápido que la velocidad del sonido no oye la explosión sónica, y mientras se mantenga a una velocidad superior a Mach 1 no oirá el sonido del motor del avión.
La rotura de la barrera del sonido es muy espectacular debido al estallido se produce, pero puede incluso apreciarse visualmente. La imagen es muy similar a los dibujos que hemos utilizado en la explicación, y en ella podemos ver perfectamente el efecto de conificación.

Los aviones comerciales que cogemos habitualmente no llegan nunca a la velocidad del sonido, pero los aviones militares llegan a superarla varias veces y suelen llegar hasta Mach 2, 3 o 4.
Algunos pueden incluso volar a Mach 7, y la lanzadera espacial que se utiliza para enviar cohetes al espacio puede alcanzar Mach 27, que significa volar a una velocidad de 33.000 km/h.