La sucesión de Fibonacci y el número áureo
La sucesión de Fibonacci es una serie de números muy conocida y muy utilizada en matemáticas, en computación y en teoría de juegos, pero es, sobretodo, muy famosa porque la encontramos muy representada en la naturaleza, y por que está estrechamente relacionada con el “número áureo”.
En realidad, se trata de una sucesión muy sencilla, que ya fue descrita hace más de 2.000 años por la matemática india. No obstante, fue mucho más tarde cuando se hizo conocida en occidente, y lo fue gracias al matemático italiano Leonardo de Pisa (siglos XII y XIII d.C.), también conocido como Fibonacci.
La sucesión de Fibonacci es la siguiente:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc.
Como podemos ver empieza con dos números “1” y a partir de ahí los números sucesivos corresponden siempre a la suma de los dos valores inmediatamente anteriores.











Pese a su sencillez, existen muchas curiosidades que la hacen bastante especial. Aquí vemos algunas de ellas relacionadas con las matemáticas:
Cualquier número entero se puede obtener con la suma de varios números de Fibonacci distintos.
De la sucesión de Fibonacci, exactamente 1/3 de los números son pares, 1/4 son múltiplos de 3, 1/5 son múltiplos de 5, etc.
Si sumamos 10 números consecutivos cualesquiera de la sucesión siempre obtendremos un múltiplo de 11.
Además, dicho número se obtiene siempre multiplicado 11 por el número que ocupa el séptimo lugar de los 10 números escogidos.
Veamos un ejemplo:
Si sumamos desde el número 2 hasta el 144:
2+3+5+8+13+21+34+55+89+144 = 374
Comprobamos que, efectivamente, es múltiplo de 11:
374 / 11 = 34
Y vemos que el 34 es exactamente la séptima cifra de las 10 de que hemos escogido al principio:
2, 3, 5, 8, 13, 21, 34, 55, 89, 144
Otra de las curiosidades que encontramos relaciona la serie con el famoso triángulo de Pascal, ya que todas las cifras de la sucesión aparecen claramente representadas en él, y se obtienen sumando sus diagonales.

Por otro lado, y como hemos comentado al inicio, lo que hace realmente peculiar a esta sucesión es su presencia en la naturaleza.
Aquí tenemos algunos de los casos más sorprendentes:
- La disposición de las semillas en los frutos:
Los piñones de una piña, por ejemplo, crecen siempre desde su base, en espirales que giran hacia la derecha y hacia la izquierda.

Y si contamos dichas espirales, resulta que el número de las que crecen para uno y otro lado son siempre dos números consecutivos de Fibonacci.

En la figura vemos claramente como tenemos 8 espirales girando hacia la derecha y 13 girando hacia la izquierda.
Y esto se cumple para piñas de todos los tamaños. Si lo comprobamos, por ejemplo, en piñas más pequeñas, veremos que suelen tener 5 espirales hacia la derecha y 8 hacia la izquierda, también números consecutivos de la serie Fibonacci.
Podría parecer que se trata de una coincidencia, pero este patrón se repite también en las semillas de la piña tropical, en el brócoli, en las hojas de las alcachofas, en los cactus, el los pétalos de las flores, etc.

Otro caso sorprendente son los girasoles, donde encontramos también sus pipas colocadas en espirales en ambos sentidos.

En los girasoles más pequeños vemos que tienen 34 espirales en un sentido y 55 en el otro, en los medianos 55 y 89, y en los más grandes 89 y 144. De nuevo todas las combinaciones son parejas de números de Fibonacci consecutivos.
- El crecimiento de ramas en las plantas y la disposición de las hojas alrededor del tallo.
En relación al crecimiento de las ramas, en muchos vegetales esta sigue los números de la sucesión de Fibonacci.
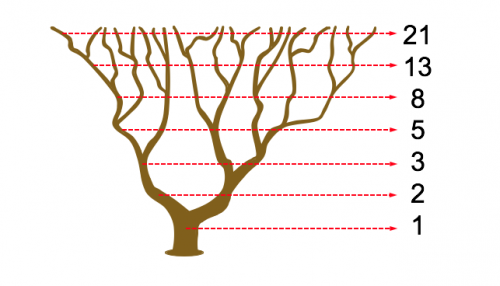
Como podemos ver en el dibujo, a medida que subimos de nivel, el número de ramas van apareciendo coincide con los números de la serie.
Si nos fijamos en la distribución de las hojas, veremos que suelen crecer en espiral alrededor del tallo, y en muchos casos también encontraremos una relación muy clara con la sucesión de Fibonacci.
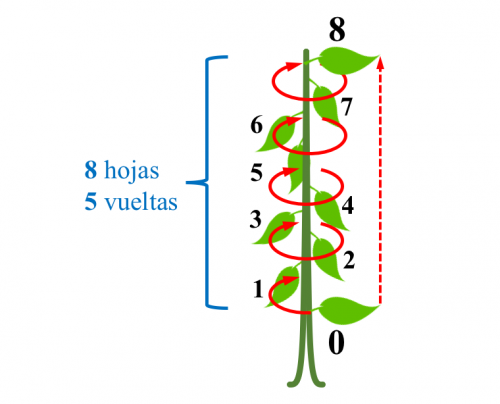
En este ejemplo podemos comprobar como, partiendo de una hoja concreta, el resto de hojas que crecen a continuación dan exactamente 5 vueltas en espiral al tallo, hasta llegar a otra hoja que se encuentra en la misma vertical que la hoja inicial.
Y si contamos la cantidad de hojas que crecen en estas 5 vueltas al tallo veremos que son exactamente 8.
De nuevo dos números consecutivos de la sucesión de Fibonacci, el 5 y el 8.
- También encontraremos la serie representada en el mundo animal y el ejemplo más famoso es el del árbol genealógico de las abejas.
Para entenderlo, en primer lugar haremos una pequeña puntualización respecto a la reproducción de las abejas.
Las abejas macho (︎♂), también llamadas Zánganos, son descendientes de una abeja hembra sin fecundar, por lo que solo tienen madre y no tienen padre.
Por otro lado, las abejas hembra (♀) son el resultado de una fecundación, por lo que tienen madre y padre.
Teniendo en cuenta esto, y desarrollando el árbol genealógico de un zángano, veremos que los números de integrantes de las sucesivas generaciones siguen la serie de Fibonacci.
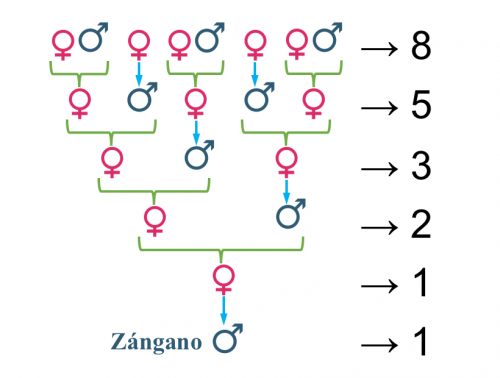
Por último, vamos a ver una representación muy peculiar de la sucesión de Fibonacci en la naturaleza. Se trata de la espiral de Fibonacci.
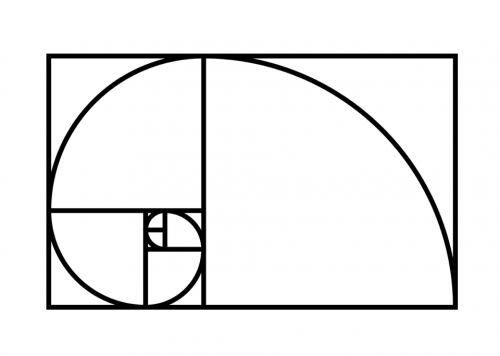
Esta espiral cumple unas características muy concretas, todos la hemos visto muchas veces y la encontramos en la concha de muchos moluscos, por ejemplo en la de los caracoles.

Pero no solo la encontramos en los moluscos, también en estructuras mucho más increíbles, como las galaxias en espiral o en la forma de los huracanes.

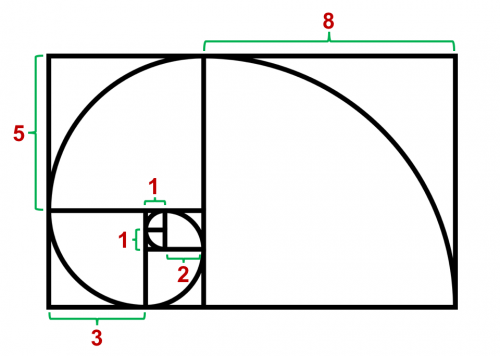
Esta espiral tan conocida está formada por la concatenación de cuadrados, que aumentan de lado siguiendo, precisamente, la sucesión de Fibonacci.
¿Y qué es el número áureo?
El número áureo es considerado un patrón de proporción perfecta basado en la relación entre dos elementos y que aporta equilibrio y belleza.
Por esta razón es también conocido como proporción áurea, razón dorada, e incluso proporción divina.
El primero en estudiar el número áureo fue Euclides en el siglo III a.C., y se trata de un número irracional que se representa con la letra griega Phi (⌽), en honor al famoso escultor griego Fidias.
Para ello Euclides partió de una recta dividida en dos segmentos.
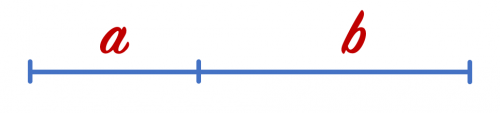
En dicha recta, la relación entre el segmento mayor con el segmento menor debía ser igual a la relación entre la recta entera con el segmento mayor.
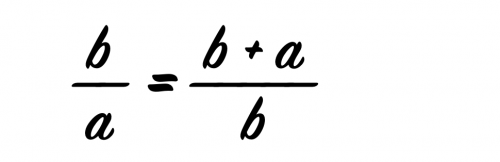
Si se cumplía esta premisa, la relación entre ambos segmentos es lo que conocemos como número de áureo (⌽).
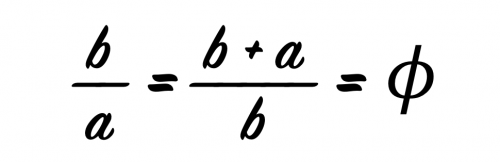
Si solucionamos la ecuación obtenemos que tiene un valor de 1,618033988…
¿Y cómo está relacionado el número de oro con la sucesión de Fibonacci?
En primer lugar cogeremos los cuadrados de la espiral de Fibonacci y dividiremos cada uno por el anterior.




Como podemos ver, en realidad estamos dividiendo cada número de la sucesión de Fibonacci por el inmediatamente anterior, y si seguimos avanzando por la serie, comprobamos que dicha división se va acercando a un número.

Y ese número es exactamente el número áureo, 1,618033988…

Por otro lado, y directamente relacionado con el número áureo, tenemos lo que se conoce como el ángulo de oro o ángulo áureo:
Si cogemos la recta con las proporciones áureas y lo convertimos en una circunferencia, veremos que aparecen dos ángulos.
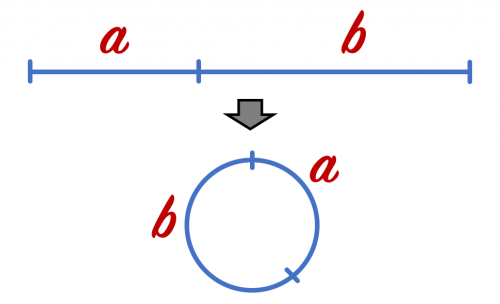
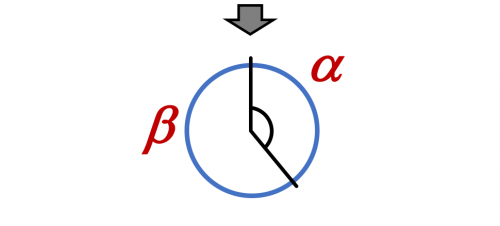
Lógicamente, la relación entre estos ángulos será también el número áureo.

Y el ángulo más pequeño (⍺) es el ángulo áureo, y tendrá un valor de:
⍺= 137,5º
¿Y dónde podemos encontrar el ángulo áureo en la naturaleza?
Relacionado con casos anteriores, lo encontramos en la distribución de las hojas cuando crecen en espiral alrededor del tallo de muchas plantas.
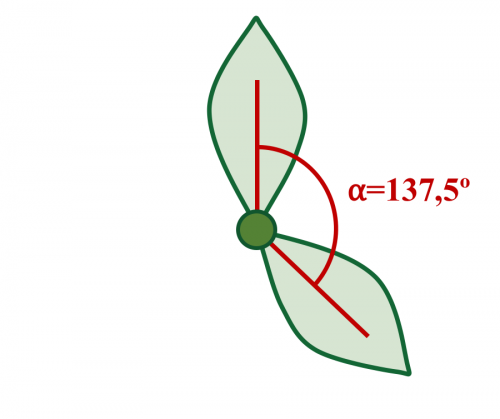
La razón es que las hojas deben distribuirse alrededor del tallo de manera que reciban la máxima luz solar, es decir, intentando que no se tapen unas a otras, y curiosamente el ángulo que optimiza la exposición al Sol de las hojas sin solaparse es, precisamente, el ángulo áureo.
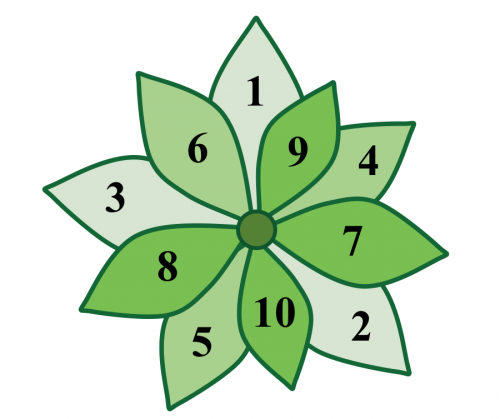
Como podemos ver en la figura, con esta disposición se consigue que un máximo de hojas quede expuestas a la luz solar.
Como hemos ido viendo la sucesión de Fibonacci nos lleva al número áureo y éste nos lleva al ángulo de oro.
Todos estos conceptos son puramente matemáticos, y sin embargo aparecen constantemente representados en la naturaleza sin que se conozca muy bien la razón por la que esto sucede.
Es por ello que la serie de Fibonacci ha resultado siempre tan enigmática.