El código binario
Ceros y Unos:
En muy poco tiempo, apenas un par de generaciones, toda nuestra vida se ha digitalizado. Ahora los teléfonos son digitales, lo libros son digitales, las cámaras son digitales, los relojes son digitales, y así casi todos los aparatos que nos acompañan en nuestra vida. En general casi toda la información que conocemos es susceptible de ser digitalizada.
Y siempre que preguntamos acerca de cómo se almacena toda esta información en los ordenadores, la respuesta es: ceros y unos, ceros y unos.
Es por ello, precisamente, por lo que hablamos de lenguaje digital; porque solo está compuesto por números, y como además se compone únicamente por dos números, ceros y unos, es por lo que se denomina código binario.
Es, sin embargo, complicado entender cómo es posible que, con solo ceros y unos, los ordenadores puedan almacenar todo tipo de información, desde textos en miles de idiomas hasta imágenes y sonidos de todo tipo.
Para entenderlo, aquí describiremos que es la digitalización de la información, y concretamente, cómo y porqué se crea el código binario.
En primer lugar, debemos darnos cuenta de que antes de que existiera el leguaje digital ya codificabamos la información de diferentes maneras para almacenarla.
Por un lado, almacenamos toda la información conceptual mediante unos códigos creados por nosotros para describir lo que nos rodea, lo que supone un código con miles y miles de símbolos distintos.
- Tenemos múltiples alfabetos y múltiples sistemas de escritura.
- Tenemos los números para las cantidades. Se trata de 9 símbolos, del 0 al 9, más todos los signos matemáticos.
- Tenemos también las notas musicales y demás símbolos para la representación de música y sonidos.
Por otro lado, para grabar la información de fenómenos físicos de la naturaleza como audio, imágenes, temperaturas, etc. utilizamos sistemas mecánicos, químicos o magnéticos, y son los que llamamos sistemas de grabación analógicos.
- El revelado de fotos se produce por un proceso químico en que los elementos del papel cambian de color según la cantidad y el tipo de luz que reciben.
- La grabación de audio y música en un disco de vinilo se produce por un proceso mecánico, mediante el cual las vibraciones del sonido quedan registradas como un surco sobre el disco.
- La grabación en cintas de cassete o video, tanto de audio como de imágenes se produce sobre una cinta magnética.
Vemos que, para ambos casos, no solo utilizamos muchos sistemas diferentes, sino que además son redundantes, ya que podemos registrar la misma información de distintas maneras.
Visto esto, podemos suponer que cualquier sistema o máquina que tuviera almacenar grandes cantidades de información siguiendo estos métodos sería extremadamente compleja.
Imaginemos, por ejemplo, una máquina con capacidad para escribir utilizando todos los alfabetos, y que además incluyera todos los soportes de grabación que hemos comentado.
Era, pues, necesario simplificar los sistemas que utilizamos para poder almacenar la información de manera eficiente, y es lo que nos condujo a la era digital.
La digitalización de la información:
La digitalización, como hemos comentado, es la conversión de la información números, y un primer paso en la digitalización sería convertirla en los números que utilizamos habitualmente.
Veamos, por ejemplo, como digitalizaríamos toda la información que almacenamos mediante la escritura. Para ello, lo único que tendremos que hacer será asignar un número distinto a cada uno de los símbolos que tenemos. Si empezamos, por ejemplo, con nuestro alfabeto, lo haríamos de la siguiente manera:
A = 1
B = 2
C = 3
…
Z = 27
Teniendo en cuenta esta correspondencia podríamos escribir cualquier palabra de un idioma que utilice el alfabeto latino mediante números, como, por ejemplo:
CASA = 3 1 20 1
Donde:
C = 3
A = 1
S = 20
A = 1
Para el caso de información proveniente de fenómenos físicos, lo que haríamos es dar un valor numérico a las diferentes intensidades de dicho fenómeno.
Por ejemplo, para almacenar datos de temperatura solo tendríamos que dar un valor numérico a la altura de una columna de mercurio para la temperatura. (De hecho, esto es más o menos lo que hace un termómetro clásico)
1 cm: 10
2 cm: 20
3 cm: 30
…
De esta manera veremos que la temperatura es “20” cuando la columna de mercurio se dilata hasta 2 cm.
Queda claro que podemos transformar a lenguaje digital todos los alfabetos, las notas musicales, los símbolos matemáticos, y cualquier otro signo y/o código que utilicemos, así como el registro de cualquier señal producida por un fenómeno físico.
Un poco más adelante veremos más en detalle como se digitaliza toda esta información.
En estos ejemplos, no obstante, estamos utilizando nuestro sistema numérico para digitalizar la información, y éste se compone de 10 dígitos, los que van del 0 al 9.
Puesto que se compone únicamente dígitos, es ya un sistema digital, pero en este caso estamos utilizando un código decimal.
Ya con esto podríamos ver un gran avance en cuanto al almacenamiento de información, ya que un ordenador podría codificar toda la información existente utilizando solamente estos 10 símbolos, lo que facilitaría mucho la fabricación y el rendimiento del ordenador.
Hemos dicho, sin embargo, que la digitalización de información que se realiza en la actualidad no convierte la información a números del 0 al 9, sino únicamente a ceros y unos. No utilizamos por tanto un código decimal, sino un código binario.
¿Por qué es necesario el código binario?
Podría parecer que la digitalización de toda la información al código decimal, es decir, a un único sistema con solo 10 símbolos, ya sería un avance impresionante, y que ya debería permitir a los ordenadores gestionar toda la información eficientemente y de manera unificada.
Existe, sin embargo, una razón técnica y práctica muy importante por la que se redujo el código decimal a código binario, y es sobretodo importante en la grabación o transmisión de la información ya digitalizada.
Volviendo al caso del sistema decimal, el ordenador que lo utilice debe ser capaz registrar o transmitir, por lo menos, diez señales diferentes.
Estas diez señales corresponden a los diez dígitos, que en realidad son una representación que utilizamos en escritura, por lo que también podrían ser también, por ejemplo, luces diez colores diferentes.

Con estos diez colores, el ordenador podría transmitir todos los números, y siguiendo el ejemplo de digitalización del alfabeto descrito anteriormente, también todas las palabras compuesta con el alfabeto latino:
Por ejemplo, si cogemos la palabra CASA digitalizada:
CASA = 3 1 20 1
Sería transmitida por el ordenador de la manera siguiente:
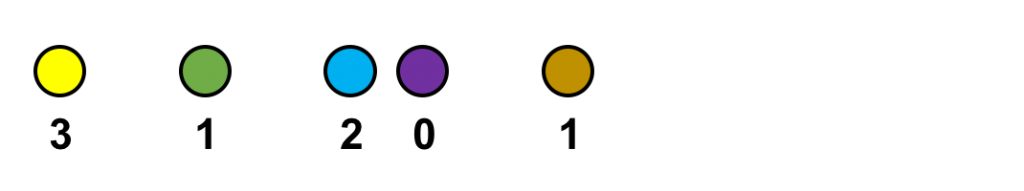
Este sería el funcionamiento de un ordenador utilizando el código decimal.
En el caso del código binario, el ordenador solamente necesitaría dos luces, ya que solo debería transmitir dos señales diferentes, una para el “cero” y otra para el “uno”.
Aquí es, precisamente, donde encontramos la gran ventaja del código binario, porque en realidad, no se necesitan dos señales distintas, sino SOLAMENTE UNA, y esto se debe a que la falta de señal ya es una señal en sí misma.
Volviendo al ejemplo de las luces, si tenemos un solo color, la luz apagada correspondería al «cero» y la luz encendida correspondería al «uno».
Así pues, simplemente encendiendo y apagando la luz ya podemos transmitir ceros y unos.

Esta sencillez es la que convierte al código binario en tan poderoso, ya que para transmitirlo podemos utilizar prácticamente cualquier elemento que pueda enviar una señal.
De hecho, al igual que con las luces, podemos utilizar simplemente el paso de corriente eléctrica como señal, con lo que el paso de corriente sería el «1» y la ausencia de corriente sería el «0».
Esta característica es la que ha permitido la impresionante evolución que han sufrido los ordenadores desde su invención.
Cada vez que se descubre un generador de señales más pequeño o más eficiente, este puede ser utilizado como transmisor de información en código binario. Actualmente se utilizan señales de eléctricas, magnéticas o incluso lumínicas, estas últimas con láser.
Una vez comprendido esto, vamos a describir como se crea el código binario, es decir, como conseguimos reducir los diez dígitos del sistema decimal a los dos del código binario.
Del sistema decimal a código binario:
Como hemos comentado, en el sistema DECIMAL utilizamos diez símbolos diferentes, desde el 0 hasta el 9 (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9).
Esto nos permite representar diez cantidades distintas usando un solo símbolo (incluyendo el 0 como una cantidad):
- Ninguna manzana: 0 manzanas
- Una manzana: 1 manzana
- Dos manzanas: 2 manzanas
- …
- …
- Nueve manzanas: 9 manzanas
¿Y cómo representamos las cantidades mayores de 9?
En este caso, como no disponemos de más símbolos, lo tenemos que hacer combinando los símbolos que tenemos.
Cuando queremos representar la cantidad «catorce”, combinaremos el 1 y el 4 para obtener el 14, con lo que:
- Catorce manzanas: 14 manzanas.
Y puesto que hay diez símbolos, combinándolos de dos en dos, podemos llegar a las cien combinaciones, y podríamos representar las cantidades de 0 hasta 99 manzanas.
ASin embargo, para continuar representando cantidades todavía mayores necesitaremos añadir otro digito. De esta manera, por ejemplo, y combinando el 1, el 4 y el 2 obtenemos el 142:
- Ciento cuarenta y dos manzanas: 142 manzanas
O combinando 7, 0 y 3, y obteniendo el 103:
- Setecientas tres 703 manzanas
Siguiendo este método, cada vez que se nos acaban las combinaciones y queremos representar otra cantidad superior, añadimos una nueva digito.
Está claro que el sistema DECIMAL es ya un código realmente efectivo ya que con solo diez símbolos podemos describir infinitas cantidades, y por eso resultó un invento tan importante.
El código binario va, sin embargo, más allá ya que nos ofrece lo mismo con solo dos dígitos, el 0 y el 1.
¿Y cómo lo hace?
Para describirlo seguiremos la misma lógica que con el sistema decimal, e iremos utilizando los símbolos de que disponemos para ir representando las diferentes cantidades.
- Para la cantidad “cero”, utilizaremos el símbolo 0
- Para la cantidad “uno”, utilizaremos el símbolo 1
Como podéis ver, ya no tenemos más símbolos para representar la siguiente cantidad, “dos”.
Tenemos, por tanto, que empezar a combinar los símbolos de que disponemos igual que hemos hecho anteriormente con el sistema decimal.
Igual que en el sistema decimal, lo ceros a la izquierda no aportan ninguna información, simplemente rellenan los espacios que no utilizamos. Es decir, el 01, el 001 y el 0001 son el mismo número; el 1.
Entonces:
- Para la cantidad “dos”, utilizaremos la combinación 10
- Para la cantidad “tres”, utilizaremos la combinación 11
Y de nuevo tenemos que añadir otra columna:
- Para la cantidad “cuatro”, utilizaremos la combinación 100
- Para la cantidad “cinco”, utilizaremos la combinación 101
- Para la cantidad “seis”, utilizaremos la combinación 110
- Para la cantidad “siete”, utilizaremos la combinación 111
Y así continuaríamos añadiendo columnas para crear nuevas combinaciones.
Como podemos ver, parece un sistema mucho más complejo que el decimal y que necesita muchísimo más espacio para representar cantidades relativamente bajas:
Por ejemplo, para representar el número 197 en código binario, escribiríamos 11000101 y para representar el 34.675 escribiríamos 1000011101110011.
La gran ventaja reside en que solo utiliza dos señales, (0 y 1), y estos cálculos para un ordenador son relativamente sencillos.
El ejemplo de las luces es realmente muy apropiado ya que lo que utilizan los ordenadores es, precisamente eso, impulsos eléctricos.
El 1 sería el impulso eléctrico y el 0 la ausencia de impulso.
Aquí tenemos algunos números en binario representados con luces apagadas y encendidas:
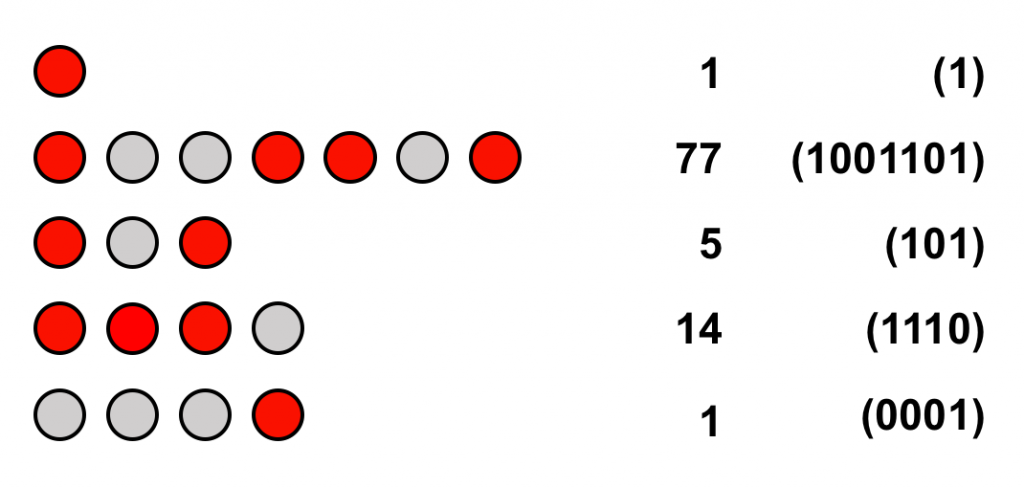
Igual que con los ceros y los unos, a medida que queremos representar cantidades mayores, necesitamos más columnas de luces.
Hemos presentado el número 1 en un sistema de una columna y también en uno de 4 columnas, y vemos como efectivamente los ceros a la izquierda no tienen valor.
Cuando vamos a escribir un número binario, por tanto, estaremos limitados por la cantidad de columnas que tengamos para rellenar con ceros y unos, exactamente igual que los espacios de una calculadora para rellenar con dígitos decimales.
Por ejemplo, en una calculadora de 8 espacios que utilice el sistema decimal, el número más alto que podemos presentar es el 99.999.999.
Cojamos los dos ejemplos que representaban un “1” en código binario, que serían, de hecho, como dos calculadoras diferentes con una y cuatro columnas respectivamente:

La primera calculadora, en código binario, solo nos permitiría llegar hasta 1, ya que solo nos admitiría un 0 o un 1.
La segunda nos permitirá llegar hasta el número 1111, que correspondería al número 15 del decimal.
Si se tratara de calculadoras decimales, la primera permitiría llegar a 9 y la segunda a 9.999.
Los ordenadores son, en realidad, calculadoras muy potentes. Por tanto, su capacidad de gestionar números más o menos grandes dependerá de los espacios que tengan para representarlos.
Las columnas o espacios para rellenar en un ordenador son los famosos bits. BIT es el acrónimo de Binary Digit (dígito binario) ya que en cada bit solo podrá haber uno de estos dos dígitos, un 0 o un 1. El bit es la mínima unidad de medida para la cuantificación de datos en un ordenador.
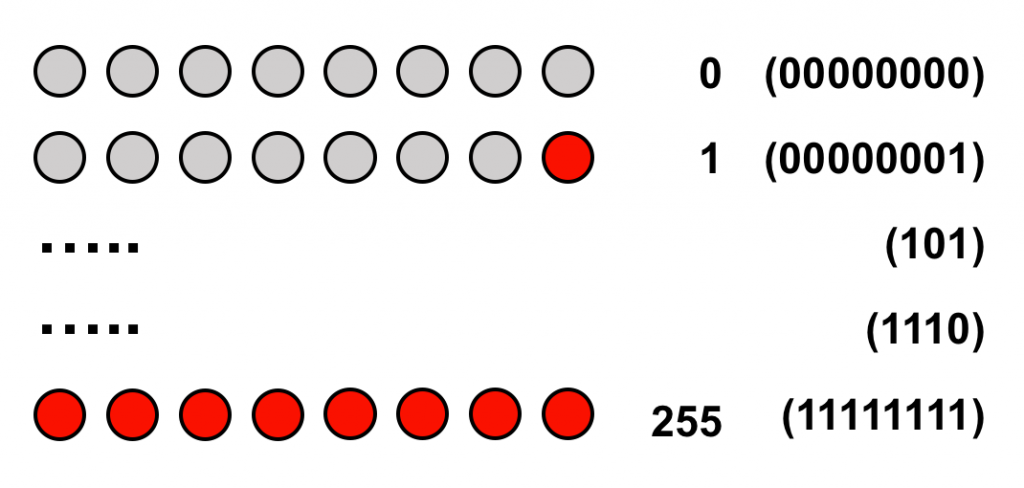
Por ejemplo, un sistema de 8 bits (8 columnas) podría calcular números binarios hasta el 11111111, que sería el 255 en el sistema decimal.
Un sistema 8 bits son lo que conocemos como un BYTE.

- 1 byte = 8 bits. Puede gestionar 255 números binarios (256 si incluimos el cero)
- 1 kb = 1024 bytes = 8.192 bits
- 1 Mb (Megabyte) = 8.388.608 bits
- 1 Gb (Gigabyte) = 8.589.934.592 bits
- 1 Tb (Terabyte) = 8.796.093.022.208 bits
2 número de bits
Como podemos ver en el listado anterior, un ordenador con 1 BITE de memoria tendrá 8 bits, por lo que podrá gestionar 28 números binarios = 256 números binarios. (255 más el “0”)
Si cogemos un ordenador con 1 Kb de memoria veremos que ya tiene nada menos que 8.192 bits, y si calculáramos los números que puede gestionar (28.192) nos daría un valor inmenso.
Para hacernos una idea de la dimensión de estas cantidades, en el caso de una memoria de 1 Tb, podríamos llegar a un número tan grande que ocuparía unos 3.000.000.000 de páginas.
Como hemos visto, es bastante sencillo obtener los números en binario; pero los números no están solo para contar, sino que realizamos operaciones con ellos; los sumamos, los restamos, los multiplicamos, etc.
Pues resulta que con los números binarios también podemos realizar todas estas operaciones, y para ello simplemente debemos tener en cuenta que son binarios.
Operaciones con código binario:
Como ejemplo realizaremos una suma de dos números binarios comparándola con la misma suma en sistema decimal:
- 11001 + 01111 = 101000 (en binario)
- 25 + 15 = 40 (en decimal)
En el sistema decimal:

En decimal, iremos sumando las diferentes columnas, y cuando una columna suma más de 9 (que es el dígito más alto), nos llevamos “1” y la añadimos a la columna siguiente.
En el caso de los binarios funciona igual, cuando una columna suma más de 1 (que es el dígito más alto en binario), nos llevamos “1” a la columna siguiente:
Recordemos cuales son los primeros números binarios. Esto nos ayudará a realizar la operación:
0 = 0 en binario
1 = 1 en binario
2 = 10 en binario
3 = 11 en binario
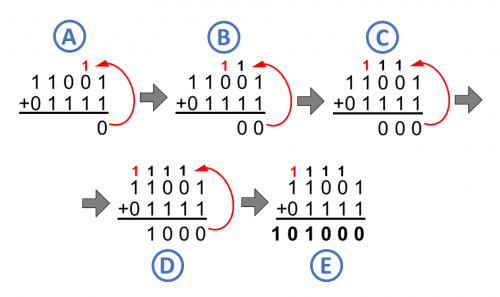
Donde:
A: 1+1 = 10, dejamos el 0 y nos llevamos «1» a la siguiente columna.
B: 1+0+1 = 10, de nuevo dejamos el 0 y nos llevamos «1» a la siguiente columna.
C: 1+0+1 = 10, de nuevo dejamos el 0 y nos llevamos «1» a la siguiente columna.
D: 1+1+1 = 11, dejamos el 1 y nos llevamos «1» a la siguiente columna.
E: 1+1+0 = 10, y finalmente añadimos la suma de la última columna.
El mecanismo para el resto de operaciones matemáticas es el mismo.
Ahora que ya sabemos cómo funciona el código binario, vemos a ver en más detalle como codifica la información comentada anteriormente, centrándonos en los textos, las imágenes y los sonidos.
En primer lugar, completaremos la explicación sobre como codifica los textos, o lo que es lo mismo, el lenguaje escrito.
Los textos en código binario:
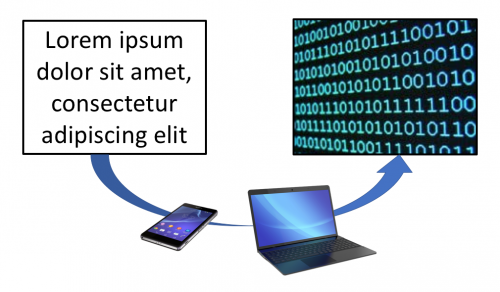
La codificación al sistema binario de los textos es, continuando con lo explicado anteriormente, muy sencilla, y se trata simplemente de digitalizarlos mediante una correspondencia entre los símbolos utilizados por los diferentes alfabetos (letras y otros caracteres) y números binarios.
Estas correspondencias están ya agrupadas por diferentes lenguajes de programación, uno de los cuales, y que nos sonará a todos, es Actionscript 2, que nos presenta una asociación de cada letra y signo con su número binario correspondiente:
A = 01000001
B = 01000010
C = 01000011
…
? = 00111111
! = 00100001
Como podemos ver el ordenador almacena textos utilizando únicamente números binarios.
Vemos, además, que Actionscript 2 nos da los números en 8 columnas, es decir, con 8 dígitos.
Se trata, por lo tanto, de un sistema 8 bits, que, como hemos visto anteriormente, solo permite codificar hasta 256 caracteres o letras.
Pueden parecen pocos, pero en realidad son suficientes para codificar el alfabeto latino al completo.
Este está compuesto por unos 128 símbolos (con pequeñas variaciones según el idioma), incluyendo letras mayúsculas, minúsculas y todos los caracteres especiales.
Esta es la razón por la que, si vamos a escribir en un ordenador en español, inglés o cualquier otro idioma que use el alfabeto latino podemos hacerlo utilizando Actionscript 2.
Por otro lado, si utilizamos otros alfabetos, como por ejemplo el chino, que tiene miles de símbolos diferentes, tendremos que utilizar un sistema que nos permita muchos más valores.
Debemos utilizar, por ejemplo, la tabla Unicode. Ésta puede tener hasta 16 o 32 bits.
De hecho, solo con la de 16 bits ya podemos asignar números binarios a 65.535 caracteres diferentes, con lo que podemos gestionar la mayor parte de los idiomas del mundo.
Para ver si ha quedado claro, vamos a ver si podemos leer un texto en código binario.
¿Qué pone aquí?
01000010–01000001–01010010–01000011–01000101-01001100–01001111–01001110–01000001
«_-_-_-_-_-_-_-_-_»

Hasta aquí hemos descrito como se codifican los números y los textos para ser almacenados en formato digital, convirtiendo toda la información a ceros y unos.
En nuestra vida diaria, sin embargo, nosotros seguimos leyendo textos escritos con nuestros alfabetos tradicionales y utilizando el sistema decimal para los números.
Esto se debe a que todos los dispositivos digitales que utilizamos habitualmente disponen también de un conversor de código binario a los lenguajes cotidianos, y lo único que hacen es aplicar la tabla de correspondencia en sentido inverso.
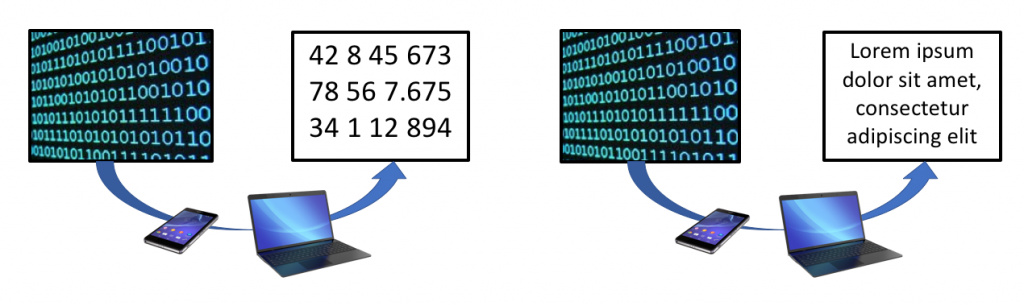
La digitalización de señales analógicas:

Ya hemos entendido como funciona el código binario en la codificación de otros códigos existentes como el lenguaje o los números, y hemos visto que el proceso es bastante sencillo.
Por otro lado, cuando hablamos de información digitalizada, también nos referimos a muchos otros tipos de información, como las imágenes, la música, la temperatura, la humedad, etc.
Toda esta información se puede medir con magnitudes físicas, como la luz, la presión o la vibración de las partículas del aire.
Estos fenómenos físicos naturales tienen una variación continua, y producen un fenómeno electromagnético que se puede representar con una función continua.
Esto es lo que llamaremos una señal analógica. Por tanto, la luz, el sonido, la energía, etc., son señales analógicas, y tendrán una representación de este tipo:
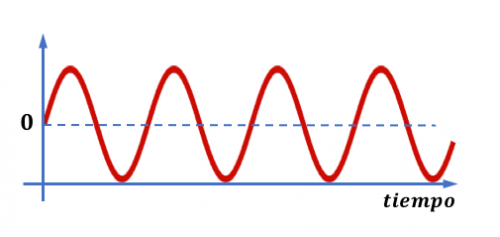
En la digitalización de estos fenómenos debemos convertir estas grabaciones analógicas al código binario, es decir, a ceros y unos.
Posteriormente, igual que con los textos, veremos que existe la posibilidad de descodificar estos ceros y unos de forma que podamos reproducir de nuevo la señal analógica original.
Empezaremos viendo cómo se realiza la grabación analógica, para la que utilizaremos sensores que registrarán físicamente el fenómeno y obtendremos la representación matemática en forma de función continua.
Es interesante ver esta primera parte de proceso ya que antiguamente la grabación era solamente analógica, y porque es muy importante para comprender su posterior digitalización.
¿Qué es y cómo funciona la grabación analógica?
Como su propio nombre indica, es una grabación análoga, por lo que transforma la señal analógica de la naturaleza en una nueva señal analógica que podemos almacenar y reproducir.
Esta grabación podrá ser mecánica, magnética o óptica.
Algunos ejemplos serían:
La grabación mecánica, se utiliza para grabar sonido en un disco de vinilo. Para ello, una pequeña aguja vibra por la onda del sonido original y va marcando con sus vibraciones un surco en el disco.
La grabación magnética es la utilizada en los clásicos cassettes, en los que el audio original se graba con marcas magnéticas en una película.
La grabación óptica, bien conocida por todos, es la que se utiliza para captar imágenes y vídeos, que quedan registradas gracias a la acción de la luz sobre un negativo fotográfico.
Una vez tenemos grabadas estas señales analógicas, para reproducirlas, simplemente tenemos que volver a transformar la grabación analógica en la señal analógica original.
Por ejemplo, al reproducir un disco de vinilo, las vibraciones de la aguja al recorrer los surcos del disco se transmiten a una membrana de los altavoces que al vibrar generan el sonido.
Ahora que tenemos una idea de cómo se realiza la grabación analógica, por lo que pasaremos a la grabación digital.
La principal diferencia es que, en vez de transformar una señal analógica original en otra señal analógica, transformaremos la señal analógica original en ceros y unos.
Recordemos, para empezar, que cualquier señal analógica se representa por una función continua.
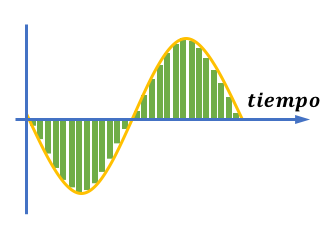
En esta función continua la altura de las curvas nos indica amplitud (A) para cada instante de tiempo (en general segundos).
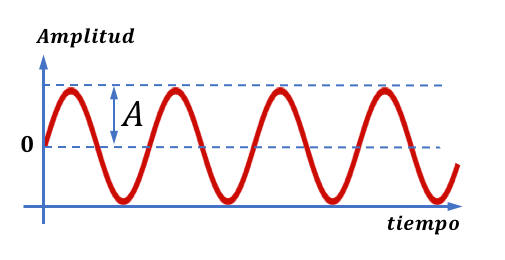
La digitalización de la señal es el proceso en que transformamos esta función en una secuencia de ceros y unos.
Esta conversión es lo que hacen la mayoría de los aparatos digitales en la actualidad, como las balanzas digítales, los termómetros digitales, las cámaras de fotos, los teléfonos móviles, las grabadoras de audio y vídeo, etc.
El sistema, igual que hacíamos con los números y los textos, será asociar un número binario a cada una de las variaciones de amplitud de la señal.
En una función continua, el rango de valores de amplitud es infinito, así que no podremos capturar exactamente la señal original en datos digitales, ya que esta captura será finita.
Por esta razón se dice que la grabación digital pierde calidad.
Esto, sin embargo, no es del todo cierto, ya que actualmente la grabación digital captura tantísima información, que lo que se pierde está muy fuera de los rangos de información que seríamos capaces de detectar con nuestros sentidos.
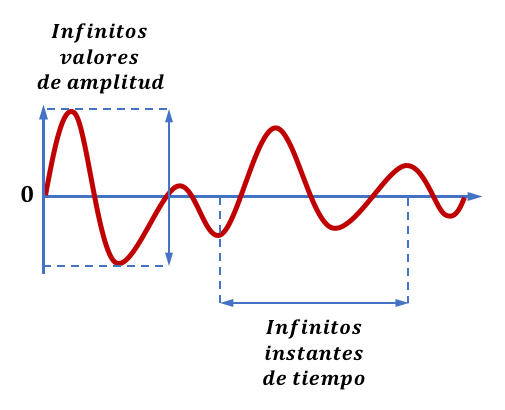
Precisamente, primer paso del proceso de digitalización de una señal analógica se llama el muestreo, y es la cantidad de muestras que tomaremos en un espacio de tiempo.
La frecuencia de muestreo afectará directamente a la calidad de la grabación digital resultante.
A mayor frecuencia, mayor calidad.
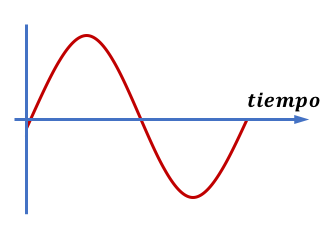
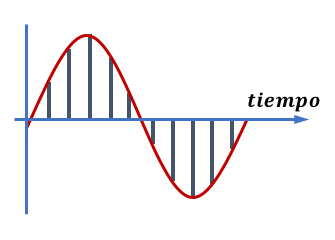
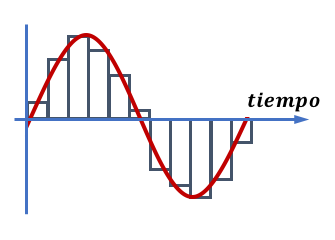
En el muestreo se escogen valores de intensidad de la señal (amplitud) a los que daremos valores numéricos utilizando el código binario. De esta manera, estos valores podrán ser leídos por un ordenador que podrá reconstruir la señal analógica.
Cuantos más valores cojamos, más la exacta será reconstrucción digital realizada por el ordenador.

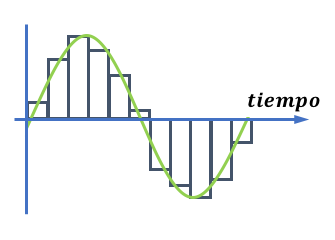
Para ello crearemos una correspondencia de valores de amplitud con números binarios.
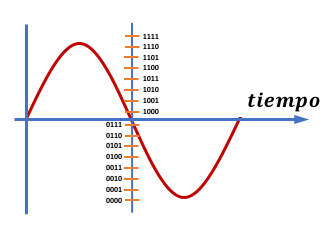
Y otorgaremos el valor binario correspondiente a cada medida del muestreo.
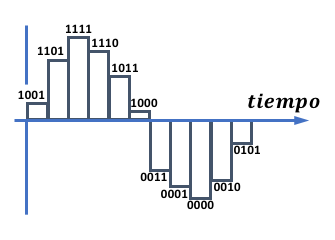
La transcripción de la señal digital del ejemplo de la figura sería:
1001, 1101, 1111, 1110, 1011, 1000, 0011, 0001, 0000, 0010, 0101
En este caso, recordando lo visto anteriormente, vemos que hemos utilizado un sistema de 4 bits. Esto nos permite tener 16 valores diferentes de amplitud, que son muy pocos, y el resultado digital tendría una calidad muy baja.
Sin embargo, existen sistemas que permiten registrar miles o millones de valores diferentes, y evidentemente, cuantos más valores de intensidad podamos registrar, más calidad tendrá la grabación digital.
Teniendo todo esto en cuenta, la calidad de la grabación en digital dependerá de la frecuencia del muestreo y de la cantidad de valores de amplitud que podamos registrar por unidad de tiempo.
Veamos algunos ejemplos:
Para digitalizar la siguiente señal analógica:
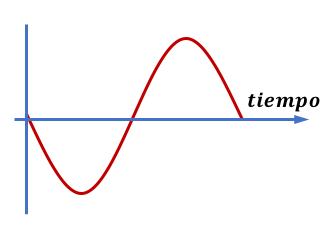
- Si la frecuencia de muestreo es alta, pero tenemos pocos valores de amplitud (sistema con pocos bits), obtendremos una grabación digital de baja calidad.
Señal analógica muestreada:
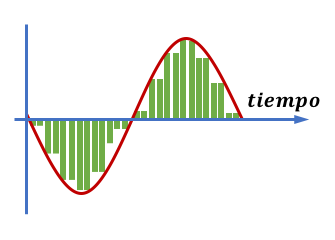
Señal reconstruida a partir de los datos digitales:
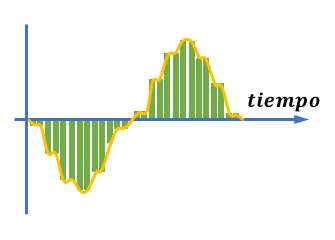
En el caso contrario, con un sistema de más bits, pero con una frecuencia de muestreo baja, también obtendremos un resultado de baja calidad.
Señal analógica muestreada:
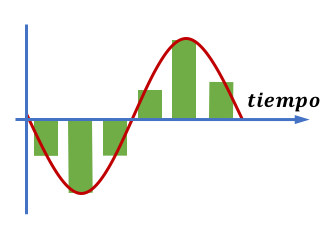
Señal reconstruida a partir de los datos digitales:
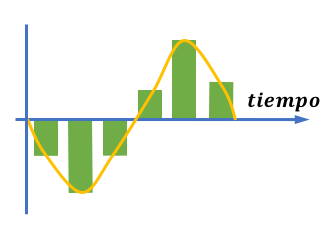
- Por último, si la frecuencia de muestreo es lo suficientemente alta, y tenemos un sistema que ofrece un gran número de valores de amplitud, obtendremos una señal de muy buena calidad que será muy parecida a la señal original.
Señal analógica muestreada:
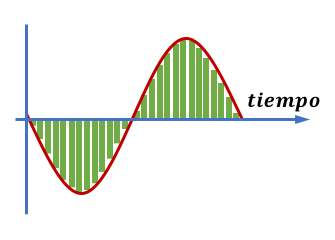
Señal reconstruida a partir de los datos digitales:
Estas reglas para la conversión de analógico a digital las podemos aplicar a todos los tipos de señales analógicas que hemos comentado: sonido, luminosidad, electricidad, presión, temperatura, etc.
Además, si la grabación en digital se realiza con una calidad suficiente, tiene grandes ventajas una vez almacenada respecto a la grabación analógica:
- No pierde calidad aunque realicemos múltiples grabaciones, ya que lo que estamos haciendo es copiar secuencias de ceros y unos.
- Ocupa mucho menos espacio, sobre todo si utilizamos formatos comprimidos, como el MP3 o el MP4.
- Permite reconstruir señales dañadas con mucha más facilidad.
Tras estos ejemplos, y una vez tenemos la señal analógica codificada en formato digital, necesitaremos realizar el proceso inverso. De eso se encargan los reproductores digitales, que leen el código binario y lo transforman de nuevo en la señal analógica.
Los casos más habituales en esta transformación digital que hemos descrito son la grabación de sonidos o música y la de imágenes o vídeo, por tanto, los vamos a ver más en detalle.
La digitalización de audios y música:
Los audios, los sonidos y/o la música son, evidentemente, una señal analógica.
Su codificación al sistema binario se realiza con el proceso anteriormente descrito para cualquier señal analógica.
Cada número binario corresponderá a un valor de amplitud, que en este caso es la amplitud de las ondas sonoras, por ejemplo, de la música.
Determinados valores de amplitud podrán, por ejemplo, corresponder a las notas musicales.
Sin embargo, en la música tenemos miles de tonos diferentes. Si queremos tener una buena calidad digital es necesario tener muchísimos valores de amplitud y realizar un muestreo con una frecuencia muy alta.
Una vez almacenado el audio en formato digital, los reproductores digitales, como por ejemplo los ordenadores, los móviles, o los reproductores de MP3, se encargan de reproducirlo mediante un conversor de digital a analógico.
En el caso del audio, convierten las secuencias de bits en una nueva señal de audio analógica, que, mediante una curva de voltaje, podremos transmitir por un altavoz.

Veamos algunos tipos habituales de grabación digital de audio:
Los CDs utilizan 16 bits para almacenar audio, con lo que pueden registrar nada menos que 65.536 valores diferentes de amplitud y la frecuencia de muestreo suele ser de 44,1 kHz, con lo que registra 44.100 muestras por segundo.
Tenemos incluso grabaciones en HD en que se utilizan sistemas de 24 bits (16.777.216 valores) con frecuencias de hasta 96.000 o 192.000 muestras por segundo (96 kHz y 192 kHz).
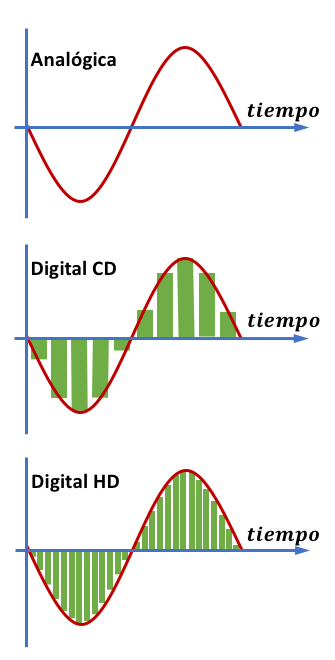
Observamos que la cantidad de valores de amplitud y las frecuencias de muestreo son realmente grandes, por esa razón tenemos unas calidades de grabación digital tan altas, y actualmente casi toda a música se almacena en formatos digitales.
La digitalización de imágenes y vídeos:

El proceso de almacenaje de imágenes y vídeos en digital, aunque parece que debería ser diferente, es también como hemos estado explicando, ya que la luz es también es una señal analógica.
De hecho, cuando hacemos pasar la luz por un prisma para dividirla en los diferentes colores que la forman, lo que hace el prisma es separar señales con diferente longitud de onda.
Y esto mismo ocurre cuando la luz del sol atraviesa las gotas de lluvia dando lugar al arco iris.
En la grabación digital de imágenes, los sensores capturan dos cosas. Por un lado, las diferentes longitudes de onda, que marcaran los diferentes colores, y las diferentes intensidades, que marcaran los diferentes tonos de cada color.

Estos puntos de captura son lo que en fotografía o vídeo digital conocemos como píxeles, y cuantos más pixeles tenga una cámara digital, más calidad obtendremos en las imágenes.
Aquí vamos a describir el proceso para un único pixel, en el que deberíamos poder registrar cualquier color existente.
Cada pixel funcionará como un pequeño ordenador, y como hemos comentado, este pequeño ordenador capturará los colores a través de la luz que recibe.
De nuevo tendremos una conversión de una señal analógica a digital y el dispositivo digital asignará un número binario a cada color.
Sin embargo, en la naturaleza existen casi infinitos colores y/o tonos, por lo que el pequeño ordenador que gestiona un píxel tendría que tener muchísima memoria.
Además, las cámaras digitales suelen tener millones de píxeles, por lo que este funcionamiento no sería posible.
Entonces, ¿Cómo lo hacen?
Aunque la cantidad de colores diferentes en la naturaleza sea tan grande, todos ellos están formados por combinaciones de tres colores primarios.
Los más utilizados en la imagen digital son el ROJO, el VERDE y el AZUL dando lugar al clásico código RGB (Red, Green and Blue).
Lo que tendremos que hacer, entonces, será utilizar estos tres colores en cada píxel para conseguir todos los demás.
Esto es exactamente esto lo que hacen las cámaras digitales; grabar un tono concreto de cada uno de los colores primarios.
Siguiendo este razonamiento, ya no necesitamos que cada píxel puede codificar millones de colores distintos. Nos bastará con que puedan codificar los tres colores primarios en diferentes tonos.
¿Y cuantos tonos de cada color primario necesitaremos?
Pues bien, el número de tonos de cada color que puede distinguir el ojo humano está alrededor de 256 (incluyendo el blanco y el negro como tonos extremos).
Necesitaremos entonces, que cada píxel pueda presentar 256 tonos para cada uno de los tres colores primarios.
Lo haremos asignando un número a cada tono. Y haremos esto para el ROJO, para el VERDE y para el AZUL.
El 0 será siempre el negro y el 255 será el color en su tono más intenso.
- 0 (negro) _ _ _ _ _ _ _ _ _ _ _ _255 (Rojo intenso)
- 0 (negro) _ _ _ _ _ _ _ _ _ _ _ _255 (Verde intenso)
- 0 (negro) _ _ _ _ _ _ _ _ _ _ _ _255 (Azul intenso)
Pero evidentemente debemos utilizar el código binario.
En este caso, para cada color primario, necesitaremos 256 números binarios para asignarlos a los 256 tonos, y como hemos visto anteriormente, para poder crear 256 números binarios necesitaremos un sistema de 8 bits.
En cada píxel tendremos, por lo tanto, 3 sistemas de 8 bits, ja que necesitaremos 256 números binarios para el ROJO, 256 para el VERDE y 256 para el AZUL.
De esta manera, combinando los tonos de cada sistema, en el píxel podremos registrar 16.777.216 colores distintos (256 x 256 x 256), que son muchos más de los que somos capaces de apreciar.
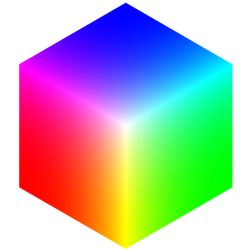
Este espectro de colores es el más común, y se conoce por “color verdadero”.
Veamos un ejemplo de color en RGB en un píxel:
Cada píxel, con sus 8 bits, registrará un tono de su color primario correspondiente.
Un Rojo muy oscuro podría ser el tono 115. En binario 00010101.

Un Verde bastante intenso sería el tono 235. En binario 11101011.

Un Azul de intensidad media podría ser el tono 195. En binario 01111000.

Y la combinación de estos tres tonos en un mismo píxel nos daría el color:

Cuyo código RGB es (115, 235, 195) en decimal, y (00010101, 11101011, 01111000) en código binario.
Aquí tenemos otros ejemplos:
Negro: (0,0,0) (00000000, 00000000, 00000000)
Blanco: (255, 255, 255) (11111111, 11111111, 11111111)
Gris: (128, 128, 128) (10000000, 10000000, 10000000)
Azul: (0, 0, 255) (00000000, 00000000, 11111111)
Magenta: (255, 0, 255) (11111111, 00000000, 11111111)
Cyan: (0, 255, 255) (00000000, 11111111, 11111111)
El negro, lógicamente, se obtiene con la falta total de colores, o lo que es lo mismo, en ausencia total de luz.
El blanco, por el contrario, es la unión de todos lo colores en su máxima intensidad, y esto se puede comprobar perfectamente en el caso del prisma, ya que como podemos ver, la luz de la cual salen todos los colores es blanca, y de hecho se llama “luz blanca”.

Una cámara fotográfica digital utilizará este mecanismo para registrar el color que recibe en cada uno píxeles que tenga, grabando así una imagen completa.
En el caso de una cámara de video digital, el proceso es exactamente el mismo, ya que el video es en realidad una secuencia de imágenes.
¿Y cómo reproducimos las imágenes una vez almacenadas en código binario?

Utilizaremos, como en el sonido, conversores de digital a analógico, que en este caso serán las pantallas digitales.
Las pantallas digitales también están compuestas por píxeles, que se corresponderán con los píxeles mencionados anteriormente de las cámaras digitales, con lo que la calidad de la imagen reproducida dependerá también de la cantidad de píxeles que la componen.

En este caso, sin embargo, lo que harán estos píxeles será descodificar la información almacenada para poder expresar los colores que componen la imagen.
Esto es posible porque que cada píxel tiene tres pequeñas lucecitas.
Cada una de estas tres lucecitas corresponderá a uno de los colores primarios, y reproducirá el tono codificado para su color correspondiente, y como los píxeles son tan pequeños, al encenderse las tres lucecitas a la vez, el color resultante del píxel será la mezcla de los tres colores.
Estos píxeles que hemos visto, de 8 bits para cada color, son los más comunes en las televisiones y los ordenadores, sin embargo, existen también píxeles que permiten todavía expresar muchos más tonos para cada color primario.
Esta capacidad de almacenar colores en cada bit se denomina “profundidad de color”, y se expresa en bits por pixel (bpp) para cada color.
En los ejemplos que hemos visto tenemos 8 bpp de profundidad de color, que como hemos dicho corresponden al color verdadero.
Existen, sin embargo, pantallas utilizadas para diseño profesional que utilizan sistemas de 10 o 12 bbp, lo que aumenta muchísimo la paleta de colores posibles.
También hay casos en que se utilizan profundidades de color más bajas, disminuyendo la calidad en el color.
Al contrario que en la música, en las imágenes es habitual utilizar intencionadamente estas calidades más bajas, tanto de resolución como de profundidad de color, buscando efectos artísticos en el resultado.
Algunos ejemplos podrían ser las fotografías en blanco y negro, en colores sepias o las fotografías con efectos pixelados.

Como hemos podido ver en todos estos ejemplos, la digitalización de información consiste realmente en codificar todo en filas de ceros y unos.
Esto, sin embargo, nos sugiere una pregunta:
Si TODA la información que se encuentra en un ordenador está compuesta únicamente por ceros y unos, ¿Cómo distinguirá un decodificador cuando debe traducirlos a números, a letras, a imágenes o a sonidos?
La única manera es indicándolo en el propio código y, de hecho, las primeras líneas de ceros y unos que un ordenador lee cuando ejecuta cualquier tarea, son precisamente unas secuencias específicas de código binario que codifican las instrucciones sobre el contenido que se va a descodificar.